Also published on UX Collective : https://uxdesign.cc/design-system-based-on-the-golden-ratio-ui-%C9%B8-e45eb98655cb
The golden number, or “phi” in reference to the sculptor Phidias, is equal to 1/2(√5+1) or about 1.618.
A short history of ɸ
The discovery of the golden section dates back to antiquity and its definition has been enriched over the centuries, including the Middle Ages.
The major contributions to mathematical research on the golden section are those of Euclid, Thales and Pythagoras, but it is undoubtedly to Fibonacci that we owe the most significant advances with his Liber Abaci, a work in which we discover the famous Fibonacci sequence, an arithmetic sequence in which the ratio of one figure to the previous one is equal to ɸ:
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 |
The expression “golden section” is a legacy of Leonardo da Vinci, who used the expression “sectio aurea” (golden section) to refer to what Luca Pacioli called divine proportion, or Kepler’s “jewel of geometry”.
Popularity of the golden rectangle
Even if the aesthetic qualities of the golden rectangle seem to be unanimously agreed upon, let’s keep in mind that it is questionable. It was in order to assess the aesthetic qualities of the Golden Rectangle by facts that Gustav Fechner, a German psychologist, conducted tests in 1874. He presented his subjects with 10 white rectangles on a black background, ranging in size from f=1 to f=2.5, each of equal area. To test his hypothesis that the golden rectangle, here f=1.62, would naturally be preferred by his panel (which was composed of people of both sexes, chosen without discriminating factors), he asked each person to choose a most popular rectangle, then a least popular rectangle. The results showed a preference for the golden rectangle, as the following results show:
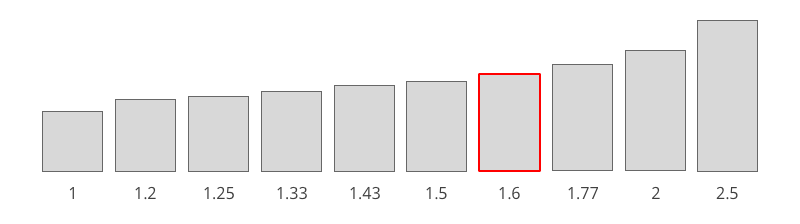
| Rapport largeur/longueur | f=1 | f=1.2 | f=1.25 | f=1.33 | f=1.43 | f=1.5 | f=1.62 | f=1.77 | f=2 | f=2.5 |
| % d’appréciation | 3 | 0.2 | 2 | 2.5 | 7.7 | 20.6 | 35 | 20 | 7.5 | 1.5 |
| % de non-appréciation | 27.8 | 19.7 | 9.4 | 2.5 | 1.2 | 0.4 | 0 | 0.8 | 2.5 | 35.7 |
(Fechner, 1876)
Since Fechner, many other researchers have re-tested the same hypothesis under different conditions. If in general the golden rectangle remains the favourite, it should be noted that this preference is rarely very marked, and never precisely on the golden ratio.
Geometric structures of ɸ
Contrary to popular belief, there is not just one golden rectangle strictly speaking. There is a rectangle whose ratio of the largest side to the smallest side is equal to ɸ. However, other constructions are possible:
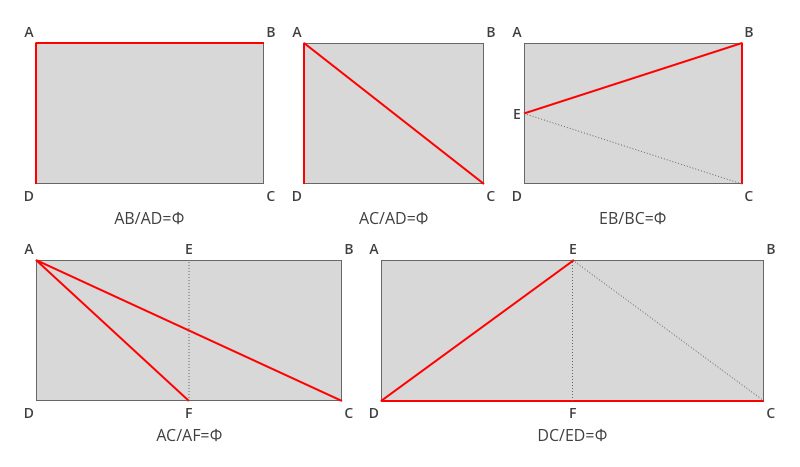
Among the non-rectangular shapes, the most popular are the regular convex pentagon and the regular star pentagon, or pentagram, in the shape of a five-pointed star. Two polyhedra, drawn from regular convex pentagons, are also famous among the geometric structures relating to the golden section: the dodecahedron and the icosahedron:
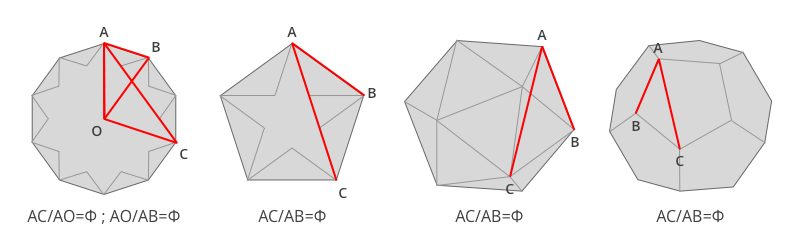
There are of course many other structures related to the golden section, such as spirals and triangles.
Presence of ɸ in nature
As for the presence of the golden section in nature, many examples are already known: sunflowers, pine cones, shells, arrangement of leaves around a flower stalk, or petals distributed in 5 points… Form golden spirals, logarithmic spirals formed from the golden section. In the same way, some crystals, whose atoms are arranged in a pentagonal pattern, are built from the golden section.
It should be remembered here that nature has two ways of producing natural phenomena from the golden section:
- by posing as a structure a pentagon, regular decagon or golden rectangle;
- by arranging the elements in a sequence of numbers similar to that of Fibonacci.
These two ways of producing elements from the golden ratio are the two ways we are gonna explore for creating an interface design from golden ratio.
Myths and realities
In order not to mystify the golden section, let us recall that while it is present in many of nature’s creations, so that a divine character has sometimes been given to this irrational number, thus making it the key to universal architecture, it should be noted that many other numbers structure the elements of nature. Scientists and mathematicians who have looked for a common structure for all the elements that make up our universe through the golden section must have been sceptical. This does not prevent mathematicians of all times from appreciating the mysterious properties of this number, nor designer-creators from making it a reference of natural aesthetics.
Geometry in architecture and design
Works designed around ɸ
In the course of history, the golden section has very often been used to structure works of an artistic, or at least aesthetic, nature. This use of the golden section has taken many different forms, with each creator or designer using it as he or she wished, without necessarily applying a defined process of use.
The Parthenon
A typical example is that the Parthenon went so far as to give its name to a variant of the golden rectangle. The relationship of the Parthenon to the Golden Section becomes evident once a golden rectangle is superimposed on the façade of the building.

The Pyramid of Cheops
Another example of the use of the golden section in the design of a major work is that it is not as easy to distinguish as in the design of the Parthenon. In order to find the golden section in the structure of the Great Pyramid of Giza, the geometry of the pyramid must be traced:
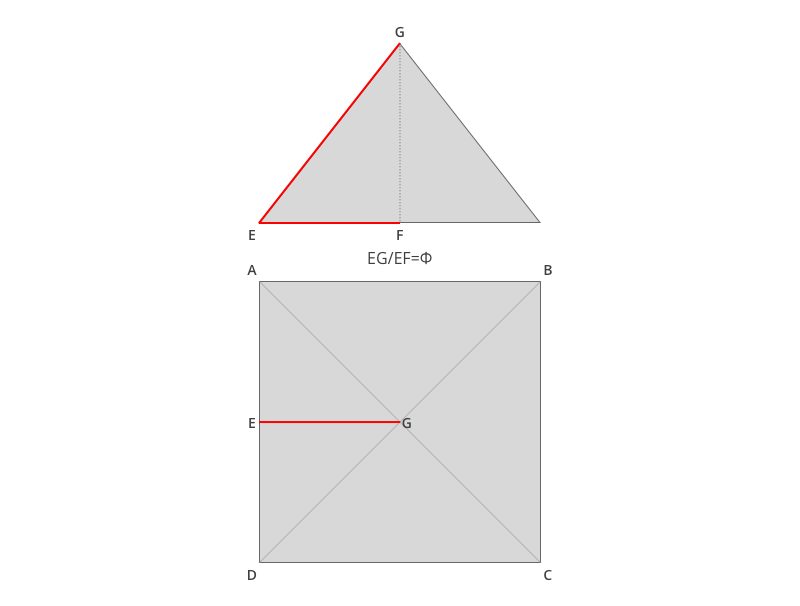
Thus it appears that the golden ratio is a key to the design of the pyramid.
Music and poetry
Many composers of music or poetry have also been bitten by the Golden Number. Because music is a series of notes structured in intervals, it has not escaped some people’s attention that these intervals may follow a pattern dictated by the golden section. The golden ratio is thus found in the 2/1 and 3/2 ratios, present in the two-beat, three-beat and four-beat rhythms. The ratio 5/3 is found in the five-beat measures. We also find the values of the Fibonacci suite.
The same applies to poetry, where the rhythm of the verses follows a mathematical pattern, an arithmetic structure, some of which have given the golden section as a key. This is the case of the famous poem Le Serpent qui danse, written by Charles Baudelaire. It is a poem in quatrains of 8 and 5 syllables in crossed rhymes. We find in this rhythm in 8 and 5 the golden proportion, as well as values from the Fibonacci suite :
| Tes yeux, où rien ne se révèle | 8 |
| De doux ni d’amer, | 5 |
| Sont deux bijoux froids où se mêle | 8 |
| L’or avec le fer. | 5 |
Tes yeux, où rien ne se révèle,
De doux ni d’amer,
Sont deux bijoux froids où se mêle
L’or avec le fer.
Charles Baudelaire, Le Serpent qui danse
Using a Key Figure in the Design Process
Le Corbusier’s Modulor
It took the famous architect Le Corbusier nearly twenty years to finalize and patent his Modulor, the key to a measurement system adapted to human morphology and inspired by historical mathematical research on the golden ratio. Intended to design architectures fully adapted to the human body, the Modulor disregards the metric system and the system of feet and inches. “The Modulor is a measurement tool derived from human stature and mathematics. A man with his arm raised provides at the determining points of space occupation, the foot, the solar plexus, the head, the fingertips, the arm being raised, three intervals which generate a golden section, known as Fibonacci. On the other hand, mathematics offers the simplest as well as the strongest variation of a value: the single, the double, the two golden sections. “(Le Corbusier, Le Modulor: test on a harmonic measurement on a human scale universally applicable to architecture and mechanics). From this example, in which geometry and arithmetic are at the service of design work, we must retain the approach that consists in systematizing design according to a mathematical key, a ratio of proportion. Here Le Corbusier relies on 3 reference keys (navel: 1.13; standing man: 1.83; standing man with arm raised: 2.26) which are linked by the ratio of proportion that is the golden ratio. From these 3 keys derive the measures he needs to design living spaces. Like other creators and designers, Le Corbusier based his architecture on a scheme dictated by the golden ratio.
Using ɸ in interface design
Posing as a structure a golden rectangle
This is the simplest way to apply the golden section to a design: draw a basic golden rectangle and then the circumscribed golden spiral. From the internal cut-out of the golden rectangle, the interface elements can be arranged according to this cut-out. A common idea is that in such a design, the focus is naturally on the target of the golden spiral, but as far as I know it have not been proven:

Making a UI design system from ɸ
Arranging the elements in a sequence of numbers similar to that of Fibonacci
First of all, let’s make one thing clear: there is no objective way to apply the golden ratio to any design. How the golden section is used and how the geometry of a design is built around it depends solely on the will of the designer.
In my case, I choose to apply the golden section not as a layer on which the elements of the design are to be arranged, but as a visual rhythm defined by an arithmetic sequence similar to that of Fibonacci.
Starting with the start: content
We start our design from the content, in this case the text. The idea is to take as a base the height of the html text we are going to use. From this height, we can define a line-height value using the golden section. To do this, it is convenient to multiply the height of the html by ɸ, quite simply:

line-height=html height*ɸ
For more informations about the use of ɸ in typography: https://medium.com/@zkareemz/golden-ratio-62b3b6d4282a
If the html object has a fixed height
It is technically complicated to really apply ɸ to a design system, for one simple reason: the limitations of the CSS3 language. More precisely, a design system truly built from ɸ would need a lot of javascript to be developed. Indeed, it would require to adjust the measures of each interface element individually, and our goal is to systematize. However, we can trick ourselves into applying ɸ to our design system while optimizing the resulting code. To do this, we have to assume that our interface elements have either a fixed height or width. In the following examples, we assume that our html element has a fixed height. In the design of my design system, I conveniently set a padding-left and padding-right equal to the height of the html content of the element under consideration.
When I create my design system, I chose to base it on the height of a content text element, here named c. From this measure c, we can extrapolate the values with which we will build our grid. To do so, we reproduce the logic of the Fibonacci sequence but starting from our key measure c:
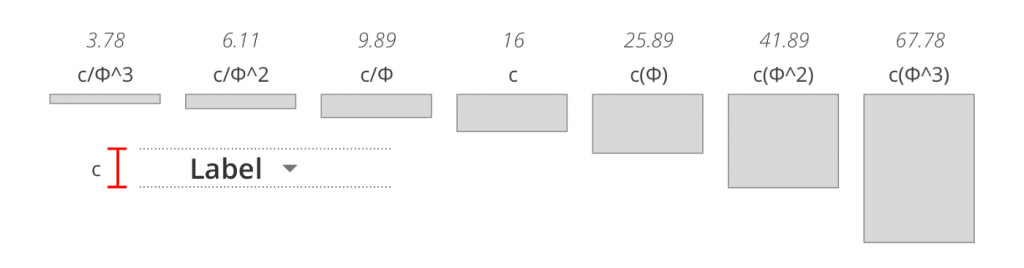
Note that adding two consecutive values gives the following value in the arithmetic sequence.
Once this is done, we build the html block linked to our text element, here a button. The padding values are derived from the extrapolated values of c. Now, from the height of this button, we can determine the values in the same logic of the Fibonacci sequence:
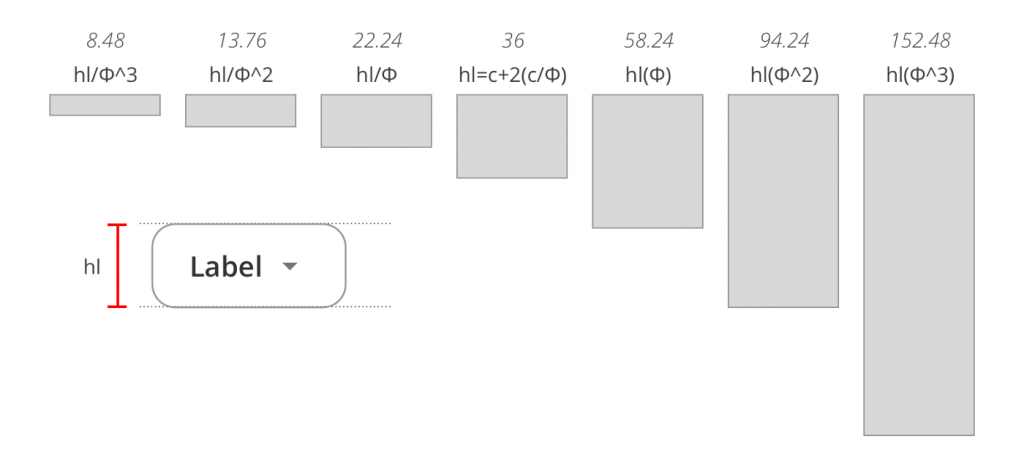
From the height of html c, we have extrapolated all the padding measures and margin of the knob:
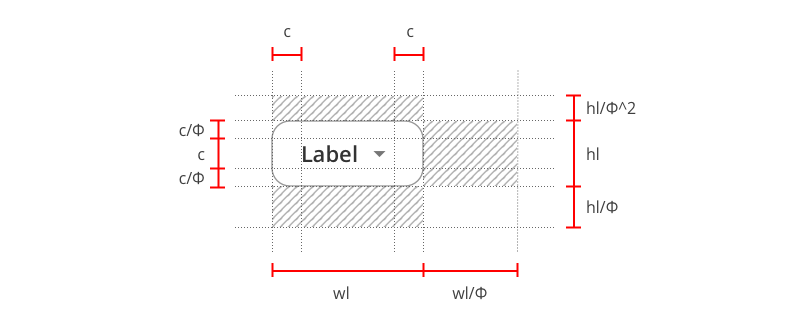
Low density:
padding-top & padding-bottom=content height/ɸ ;
margin-top=button height/ɸ^2
margin-right=button width/ɸ
The result seems satisfactory to me. What do you think?
If the interface requires a high density of information
From experience, it is often necessary to vary the density of information on a page, especially when developing interfaces for business software containing tables and many possible actions. In this case, we can densify our button by choosing more or less advanced values on our value sequence. For example, instead of calculating c/ɸ, we will calculate c/ɸ² or c/ɸ³, etc. Conversely, we can flare our block by calculating cɸ², cɸ³, etc.

High density:
padding-top & padding-bottom=content height/ɸ ^2;
margin-top=button height/ɸ^3
margin-right=button width/ɸ^2
Limitation of the height and minimum width of an html object
Of course, not all measurements given to the interface elements can be relative. Every interface has constraints, starting with the minimum height and width that an interactive element must have in order to be used comfortably on a touch screen. For my part, I set this value at 40*40px. Thus, some of my elements cannot simply be entrusted to the Golden Number; it is necessary to check that these constraints are respected.
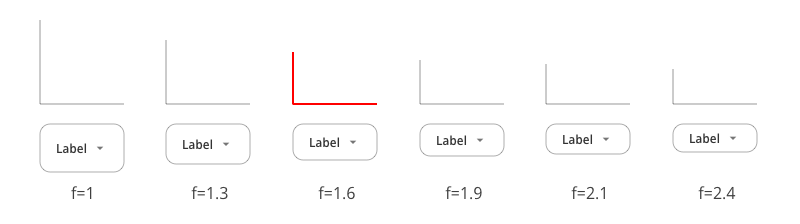
Other usable ratios
And if you don’t appreciate the aesthetics offered by this use of the golden section, why not try using another function value? Here are some examples of buttons made with different values than ɸ:
The design system today
With this method I made a full design system based on golden ratio. I am using this design system today in my professional productions, for both B2C and B2B products, with the large and small density information system.